Hexo
0%

算法：哈希函数和哈希表

发表于 更新于 分类于

哈希函数和哈希表

哈希函数的特点

  1. 一般情况下，输入域无穷，输出域有限

  2. 相同的输入参数，一定会返回相同的值（内部不随机）

  3. 因为输出域可能小于输入域，所以不同输入可能有相同输出（def：哈希碰撞）

  4. 离散性：即便输入参数有一点点不一样，输出的值也有可能不一样

    均匀性：假设输出域为S，很多个输入，映射到输出域，在输出域内任意选择一块区域，选中的输出点个数几乎一样

    假设输入：in1,in2,in3……

    输出为：out1,out2,ou3……

    如果输出为均匀的，那么将输出值%m之后，结果在0~m-1上也是均匀的

例1：小内存返回大文件中出现次数最多的

一个文件存放无符号整数，总共有40亿个，只有1G内存，返回出现次数最大的数

Q：使用简单的哈希，有可能出现内存不足

​ 因为一条记录<int,int>至少占用8字节，则40亿数的哈希表至少占32G

解法：

40亿数—>哈希函数—>%100—>0~99 （哈希函数的作用：使数据均匀分布）

相当于把一个40亿的大文件划分为100个小文件，由于哈希函数的均匀性，所以哈希值再取模以后一定是均匀分布在0~99

再依次读取小文件，建立每个小文件的哈希表，因为是均匀分布的，所以一个小文件的哈希表大小=32G/100

哈希碰撞的解决方案：

  1. 链表式解决

  2. 开放寻址法

    1. 线性探测法：碰撞发生时，元素存储位置+1直到找到未占用位置

      ——>问题：导致“二次聚集”：不同基地址的元素争夺同一个位置

    2. 平方探测法：为了避免上述问题，重新寻址时，位置+1，+4……+(冲突次数)^2

  3. 再哈希法

    遇到位置被占用，对该位置进行再次哈希，循环直到找到未占用的位置

    注意：控制再哈希的次数阈值，不然可能出现无限循环的情况，导致查找元素时无法确定边界，即不知道进行几次哈希才算找不到元素

哈希表的实现

先进行哈希，再模一个数确定放在哪个桶里

当单向链表过于长时，影响查找效率，对哈希表进行扩容——>哈希表大小变为原来两倍，则单向链表长度变为原来一半（哈希函数的均匀性）

布隆过滤器

问题：黑名单问题

要求一个集合：增加和查询，不需要删除操作，且允许一定失误率（这种失误指的是把白误报成黑，不会出现把黑误报成白）——宁可错杀，不可放过

布隆过滤器：减少内存空间，但带来了一定的失误率

位图

——bit类型的数组

实现方式：拿基础类型拼

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
int *arr = new int[10];//4*8*10=320bits
//arr[0]——int[]0~31
//arr[1]——int[]32~63

int i = 178;//取得178bit的信息：0/1
//定位
int numIdx = i / 32;
int bitIdx = i % 32;

//取得i位置的信息
//为什么是32，因为1个int是32bit
int status = ((arr[numIdx] >> bitIdx) & 1);
int bit = (arr[i / 32] >> (i % 32)) & 1;

//将状态改为1
arr[numIdx] = arr[numIdx] | (1 << bitIdx);

//将状态改为0
arr[numIdx] = arr[numIdx] & (~(1 << bitIdx));

布隆过滤器的实现

（1）黑名单的建立

准备一个大的位图长为m，k个哈希函数

url1—f1—>m1 m1位置涂黑

​ —f2—>m2 …… —fk—>mk ===>m1,m2,……mk位置涂黑

…… …… ……

urln===>k个位置涂黑

ps：白的描黑，黑的别管

黑名单建立完毕

（2）黑名单的查找

比如说要查找urlx ===》 经过k个哈希函数再%m得到k个位置

如果这k个位置都为黑，则输出urlx属于黑名单

为什么黑不会报为白？只要urlx是黑的，则k个位置一定是黑的，报为黑名单

有可能白报为黑？例如m值很小，有可能位图全黑，误报率增加

（3）失误率的决定因素

  1. 主要因素：m值

    m太小，导致黑名单建立过程中都被涂黑了，失误率提高

  2. 第二个因素：k值

    相当于一个样本采k个特征点，所以一定程度上，k值越大，误报率越低

    但如果k值太大，同样会导致位图上涂黑的地方过多，提高误报率

    所以，先选取合适的m值，再根据m值选取合适的k值来降低误报率

（4）布隆过滤器参数选择

  1. 确定模型：是不是类似于黑名单问题，只需要添加和查询，不需要删除操作

  2. 确定是否允许失误率

  3. 布隆过滤器的设计只跟两个因素有关：n=样本量，p=失误率

    注意：跟单样本的大小没关系，因为放到布隆过滤器的值是哈希之后再模的，所以只需要保证单样本的大小属于哈希函数的输入范围

    结果都向上取整
    $$
    m=-\frac {n\ln p} {(\ln 2)^2}\
    k=\ln 2    \frac {m}{n}\approx0.7*\frac {m}{n}
    $$
    上述取到的是理论值。

    由实际的m，k值可得到实际的失误率p
    $$
    p=(1-e^{-\frac {(n*k)}{m}})^k
    $$

一致性哈希

分布式服务器

假设有三台数据库服务器m1 m2 m3

data1——哈希 %3——m1 数据1放在m1里

…… …… ……

负载问题：如果有的数据高频，有的数据低频，导致服务器负载不均衡

哈希key的选择

===》题外话：哈希key的选择

​ 可以：身份证、人名

​ 不可以：国家名、性别

——》高频、中频、低频都有数量——》三台服务器负载均衡

例：以性别为哈希key会导致两台服务器在工作，另一台服务器负载为0

一致性哈希

下一个问题：

这种服务器选择方式——data==》哈希==》%服务器数量==》数据存放位置

带来问题：当增加服务器或者减少服务器，数据迁移是全量的，也就是说所有数据都要重新计算哈希值再模运算

解决====》一致性哈希

例：某种哈希算法得到的哈希值取值范围形成一个环0~x，数据得到的哈希值打在环上

计算机器的哈希值：m1 m2 m3 m4

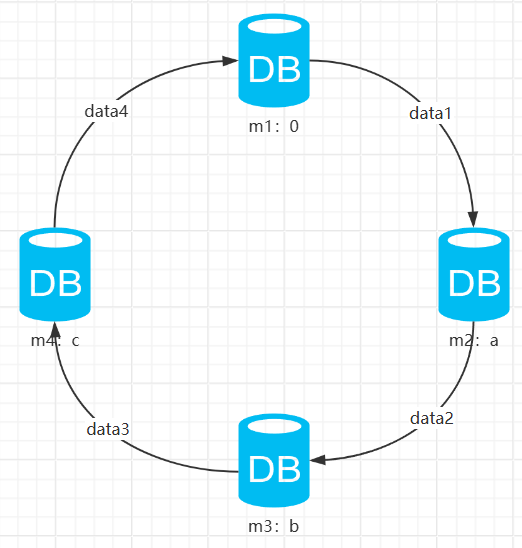
image-20240621170814015

数据存储：数据==哈希==》data ——》插在环上，顺时针最近的就是数据存储的数据库，例如：data1放在m2上

所以在逻辑服务器上：m1 [c , 0] m2 [0 , a] m3 [a , b] m4 [b , c]

所以在逻辑服务器上存储：0 a b c，插入数据data=》计算哈希值datam=》通过二分查找找到>datam最左边的数==》找到存储位置

  • 数据库增加，例如：增加m4，原来[b , 0]归m1管，现在分一部分[b , c]给m4管，所以只需要重新计算m1上的数据的哈希值
  • 数据库减少，例如：减少m4，只需要把m4上的数据放到m1上就行

===》问题：当机器数量较少时，服务器分布是不均匀的也会导致负载不均衡的情况

虚拟结点

解决办法：虚拟结点

m1：a1,a2……a1000

m2：b1,b2……b1000

m3：c1,c2……c1000

实际上去抢环的是虚拟结点，数量多==》环上有3000个点==》数据分布均衡

数据选择存放在哪个点——》存放在哪台服务器上

并且，这种方式还可以管理负载：比如，实际服务器a性能号，b性能差===>给a分配2000个虚拟结点，b分配500个虚拟结点