Hexo
0%

算法：KMP

发表于 分类于

KMP算法

KMP算法：查找连续子串，返回值：str1中str2开始的位置/-1

例：str1：ABCD1234de

​ str2：1234 返回值：4

​ str3：1234e 返回值：-1

暴力解法：遍历str1，看每个开头能否配出str2

时间复杂度：O（mn）

KMP算法基础：next数组

——str2中每个字符对应一个信息：最长公共前后缀（该字符前面的字符串相等前缀和后缀的最大长度，并且不能取到整体）

例：abbabb k k==>3

长度 1 2 3 4 5 6
前缀 a ab abb abba abbab 不讨论
后缀 b bb abb babb bbabb
!= != == != !=

所以str2对应一个next arr==》用来加速匹配过程

例：str2={a,a,b,a,a,b,s}

next={-1,0,1,0,1,2,3} ps：next[0]=-1(人为规定)，next[1]=0

KMP算法实现原理

——目的：让i跳的尽可能快（经典：i=i+1）

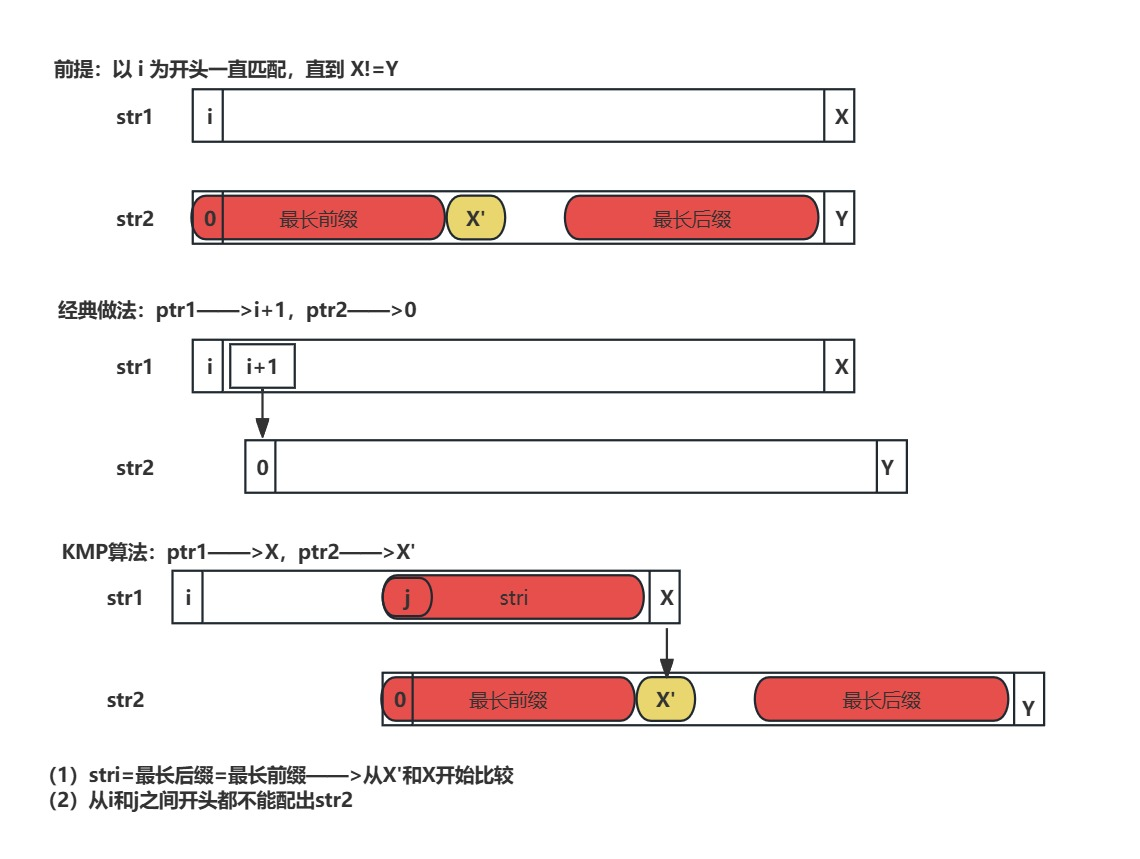
image-20240624223723044

（2）的证明通过反证法：设k在i~j之间，k开始能配出str2……推出跟最长公共前后缀矛盾

next数组的求法

求next[i]

找next[i-1]==》前缀的下一位？=next[i-1]

相等：next[i]=next[i-1]+1

不相等：cur再往前跳，来到cur对应前缀的下一位（next[cur]），判断跟str[i-1]是否相等

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
//O(M)
vector<int> getNextArray(string str) {
	int size = str.size();
	if (size == 1) {
		return { -1 };
	}
	vector<int> next(size);
	next[0] = -1;
	next[1] = 0;
	int i = 2;//当前要求next数组位置
	int cur = 0;//跟i位置比较的位置，0：next[1]=0(cur=next[i-1])
	while (i < size) {
		if (str[i - 1] == str[cur]) {
			//next[i] = cur + 1;//next[i-1]+1
			//i++;
			//cur = cur + 1;
			next[i++] = ++cur;
		}
		else if (cur > 0) {
			cur = next[cur];
		}
		else {
			next[i++] = 0;
		}
	}
	return next;
}
//str1长N，str2长M,N>=M
//时间复杂度：O（N）
int KMP(string str1, string str2) {
	if (str1.empty() || str2.empty() || str1.size() < str2.size()) {
		return -1;
	}
	vector<int> next = getNextArray(str2);//O(M)
	int ptr1 = 0, ptr2 = 0;
	//O(N)
	while (ptr1 < str1.size() && ptr2 < str2.size()) {
		if (str1[ptr1] == str2[ptr2]) {
			ptr1++;
			ptr2++;
		}
		else if (ptr2 == 0) {//相当于next[ptr2]=-1
			//str2[ptr2]!=str1[ptr1],str1第一个都不匹配
			ptr1++;
		}
		else {
			ptr2 = next[ptr2];
		}
	}
	//ptr1越界—-1，ptr2越界—匹配完成
	return ptr2 == str2.size() ? ptr1 - ptr2 : -1;
}
int main() {
	string str1 = "abcd1234";
	string str2 = "1234";
	string str3 = "1234e";
	cout << KMP(str1, str2) << endl;
	cout << KMP(str1, str3);
}