Hexo
0%

差分密码分析

发表于

有两种适用于对称密钥分组密码的攻击——线性密码分析和差分密码分析，基于基本替换置换网络密码basic Substitution-Permutation Network cipher，被选为AES的Rijndael密码是从基本的SPN结构派生的

A Basic Substitution-Permutation Network Cipher（基本的替换-置换网络密码）

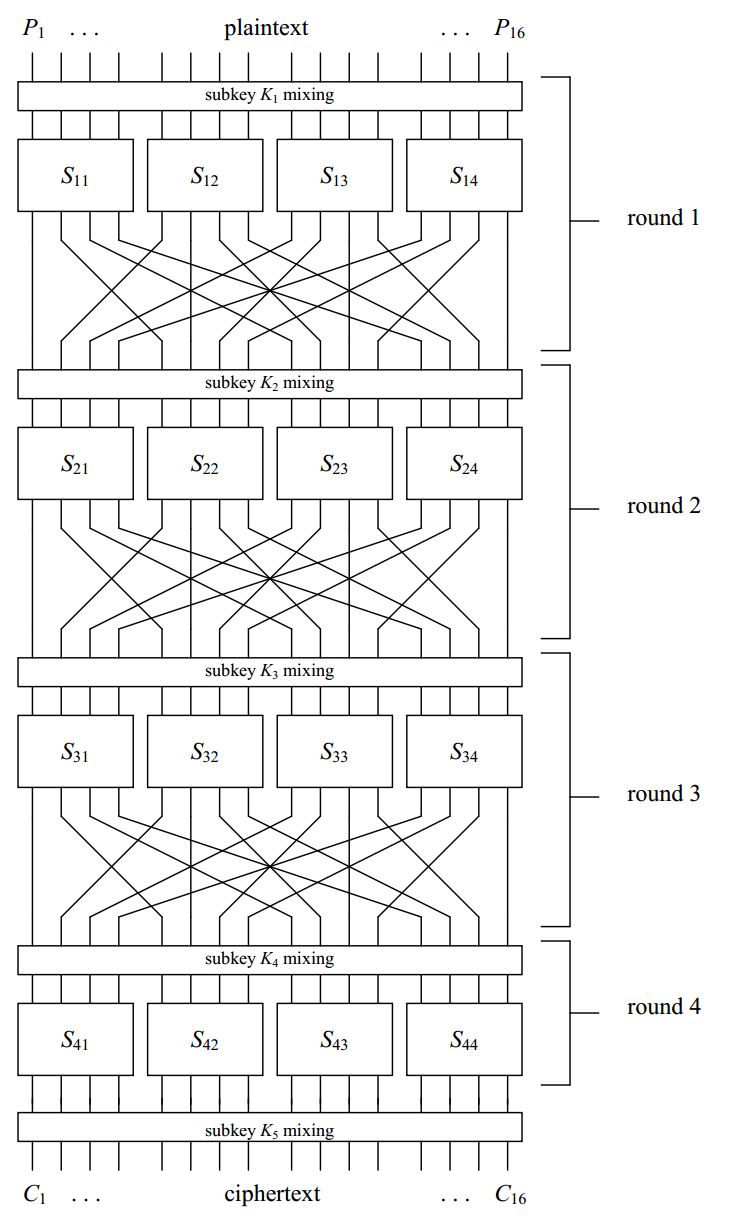
Substitution替换

Our cipher：

  1. 16bit datablock——>4个4bit sub-blocks

    • 一个sub-block是一个4*4的S-Box的输入
    • 4*4的S-Box指的是4bit输入到4bit输出的的替换
    • 用一张16个4bit值表示的表
    • 特点：非线性，即输出bit是不能用对输入bits的线性操作表示

  2. 所有S-Boxes使用相同的nolinear mapping

    在DES里每一轮使用的所有S-Boxes不同，但所有轮次使用相同的S-Boxes集合（相同几个S-Boexes但顺序不一样）

    • 线性和差分密码分析的攻击同样适用于：使用一种mapping或者所有S-Boxes使用不同mappings

Permutation置换

置换：bit位置的置换

Key Mixing

  • To：实现密钥混合——在与轮相关的key bits（也叫子密钥）和每轮输入的数据块之间使用按位异或
  • To：最后一轮替换不会轻易被分析者忽略——在最后一轮替换之后也应用subkey mixing
  • 密码的主密钥master key——密钥调度key schedule——>一轮的子密钥subkey

Decryption

解密也采用SPN的形式

  1. 解密网络中的S盒中使用的映射是加密网络中映射的逆
    • 所以为了使SPN允许解密，所有的S-Box必须是双射的，即输入和输出一对一映射
  2. 子密钥以相反的顺序应用
  3. 总之，数据流反过来就是了

Differential Cryptanalysis

——差分密码分析在基本SPN密码中的应用

Overview of Basic Attack基本攻击概述

差分密码分析利用明文差异和差异在密码最后一轮中高概率出现的特点，即通过观察成对的明文和相应的密文之间的差异来揭示加密算法的内部结构

X’——>Y’，X”——>Y”
ΔXi = Xi’ ⊕ Xi” （按位异或）
ΔX = [ΔX1 ΔX2 … ΔXn]
ΔY = [ΔY1 ΔY2 … ΔYn]

  • 对于理想化的随机密码，给定ΔX，出现ΔY的概率是1/2^n
  • 差分密码利用：对于给定的ΔX，会有一个Δy出现的概率很高。这样一对（ΔX,ΔY）视为一个differential

差分密码分析是一种选择明文攻击，这意味着攻击者能够选择输入、检查输出，以此来获得密钥。
攻击者将选择一对输入X’X”，满足特定的ΔX，因为对于这个ΔX，会有一个ΔY高概率出现

本文研究一个differential的构造：by检查高可能差分特征（differential characteristics）

差分：一对输入的明文差异 + 高概率出现的密文差异

差分特征：一轮的输入和输出差异

  • differential characteristics：一轮的输入和输出差异的序列
  • 一轮的输出差异对应于下一轮的输入差异
  • 使用highly likely differential characteristic让我们有机会获得进入最后一轮密码的信息，To derive bits from the last layer of the subkeys

To 构造 highly likely differential characteristics

  1. 检查单个S-Box的properties，并使用这些属性来确定complete differential characteristic——考虑S-Box输入和输出的差异，来确定一个high probability的差异对
  2. 对每轮的S盒差异对进行组合，使一轮的output difference bits对应下一轮的input difference bits——>找到一个high probability differential（明文差分+the difference of the input to the last round最后一轮的输入）
  3. 由于子密钥涉及两个data sets（作用在输入X’和作用在输入X”），异或之后子密钥实际上会被抵消掉，所以他们并不出现在最终的差分表达式中。因此，差分密码分析的优势：允许绕过子密钥进行直接求解

Analyzing the Cipher Component密码组件分析

To检查S-box的difference pairs

对于4*4的S盒：4位输入，4位输出——16个X的值

只需要考虑X’的16个值+给定ΔX — 可以得到X” = X’ ⊕ ΔX
例：∆X值为1011、1000和0100时：表中，∆X = 1011出现∆Y = 0010的次数是16个可能值中的8个（即概率为8/16）；在给定∆X = 1000的情况下，∆Y = 1011的出现次数为4/16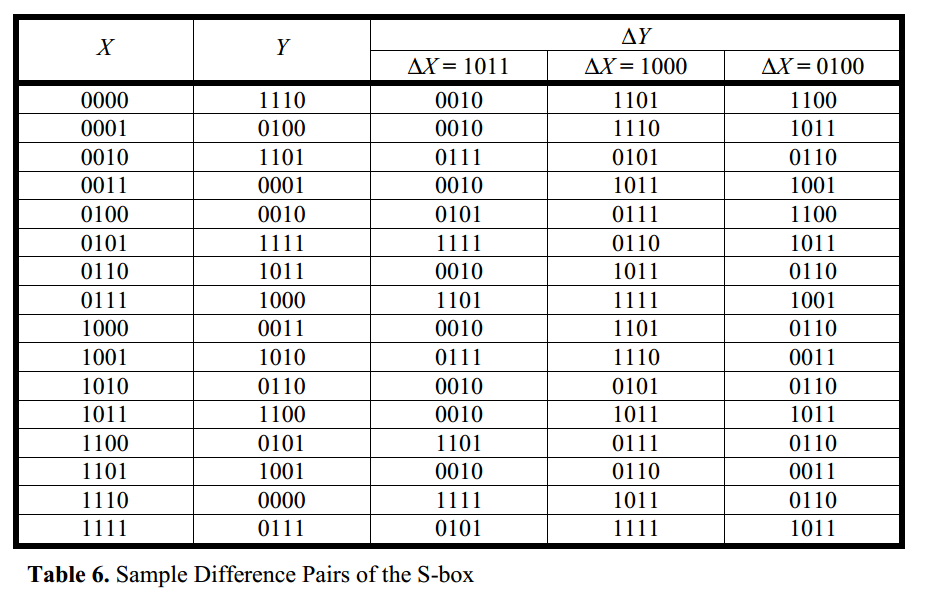

我们可以将S-box的完整数据用差值分布表制成表格，其中行表示∆X值，列表示∆Y值。差值分布表如下，表中的每个元素表示给定输入差∆X的对应输出差∆Y值的出现次数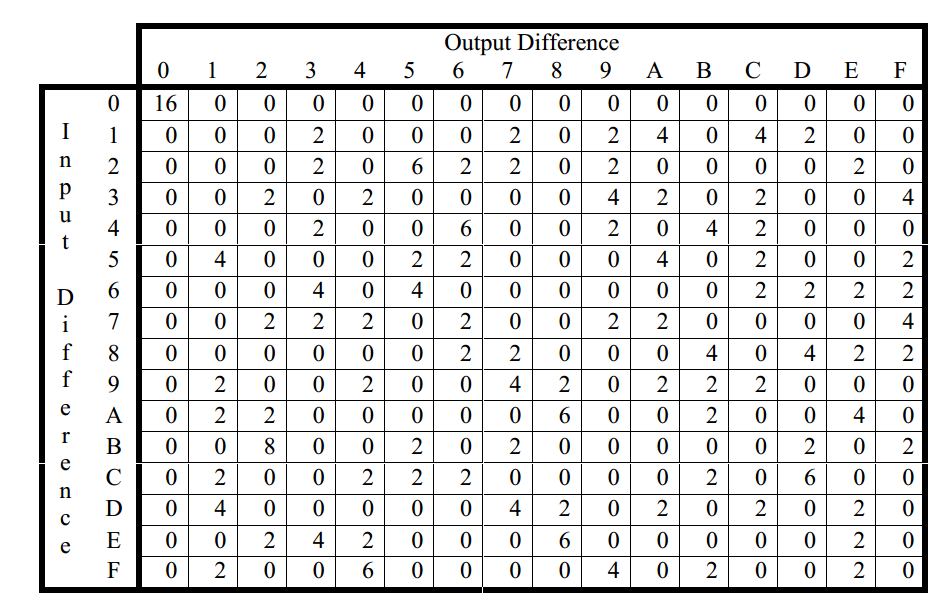

差值分布表的性质：

  1. 一行和一列所有元素的和是2^n=16
  2. 所有元素值都是偶数：因为ΔX对应于成对的输入（X’⊕X”和X”⊕X’），所以一个ΔX对应成对相同的ΔY，所以ΔX对应于任意的ΔY个数为偶数

理想的S-box，差值分布表所有元素都为1，与性质矛盾，所以理想的S-box是无法实现的

密钥对S盒差分的影响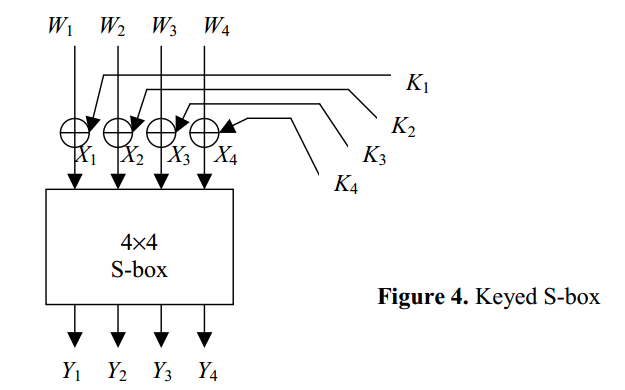

无密钥时，输入为X，输出为Y
有密钥时，输入为X⊕K=W
所以输入的差分 ΔW = [ΔW1 ΔW2 … ΔWn] （ΔWi = Wi’ ⊕ Wi”）
ΔWi = Wi’ ⊕ Wi” = (Xi’ ⊕ Ki) ⊕ (Xi” ⊕ Ki) = X’ ⊕ X” = ΔXi
所以密钥位对于输入差值没有影响，也就是说：有Key的S-Box和无Key的S-Box具有相同的差值分布表

Constructing Differential Characteristics构建差分特征

一旦为SPN中的S盒编译了差分信息，就可以得到整个密码的有用差分特性的数据

通过连接适当的S盒，在每轮中构造某些S盒差分对的差分特征，使得差分涉及到最后一轮S盒的明文对和数据位的输入，可以通过恢复最后一轮之后的子密钥位的子集来攻击密码

差分特征构造的例子

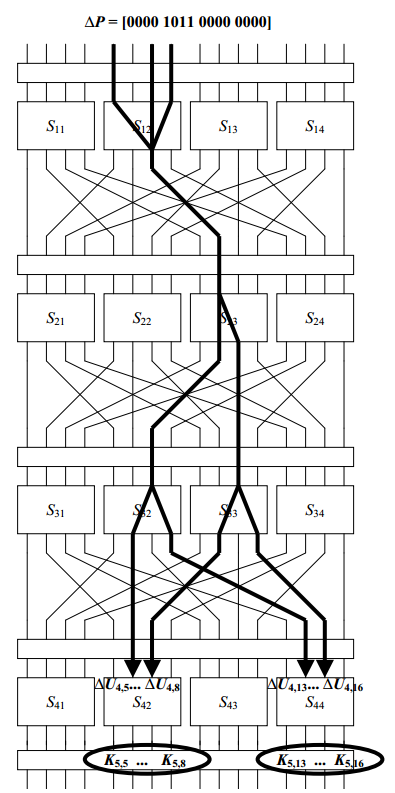
image-20241210185038908

考虑一个涉及S12、S23、S32和S33的差分特性：

∆P：明文差异

∆Ui：第i轮S盒的输入

∆Vi：第i轮S盒的输出

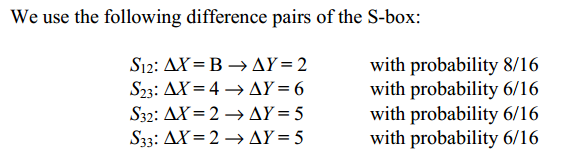
image-20241210185345969

∆P = ∆U1 = [ 0000 0000 1011 0000 ]

∆V1 = [ 0000 0010 0000 0000 ]

对于给定∆P（假设所有轮次的S盒的差分对之间是独立的，所以概率直接相乘）：

有8/16概率得∆U2 = [ 0000 0000 0100 0000]

有8/16 * 6/16 = 3/16的概率得∆U3 = [ 0000 0010 0010 0000]

有8/16 * 6/16 * 6/16 * 6/16 = 27/1024的概率得∆U4 = [ 0000 0110 0000 0110]

在密码分析过程中，许多对明文∆P = [ 0000 0000 1011 0000 ]将被加密，会有27/1024的高概率出现所示的差异特征，def：满足∆P的明文对称为 right pairs， 没有这种特征的明文对称为 wrong pairs

Extracting Key Bits提取密钥位

一旦以足够大的概率发现R轮密码的R−1轮差分特征，就可以通过恢复最后一轮子密钥来攻击密码。在我们的示例中，将从子密钥K5中提取比特，将跟在被非零差异影响的最后一轮S盒之后的密钥认为是target partical subkey。

过程包括：尝试目标子密钥位的所有可能值，将其与密文进行异或并通过S盒反向运行数据，如果得到的值和期望值一样，计数+1，最大计数对应的是正确的子密钥。

对示例密码的攻击：

  1. 差分特性在最后一轮影响了S42和S44的输入，所以[K55,K56,K57,K58,K5 13,K5 14,K5 15,K5 16]是目标子密钥位
  2. 尝试与∆P对应的每个密文对，对于每个密文对都尝试目标子密钥位的256个值（2^8），通过S42和S44反向运行得到S盒的输入，与期望的∆U4比较，一样计数+1
  3. 最大的计数被认为是正确的值

注意：没有必要对每个密文对执行部分解密。因为最后一轮的输入差只影响2个S盒，因此当特征发生时（即输入的是 right pairs），S41和S43的密文位差必须为零，通过这个条件过滤掉一些 wrong pairs，不用进行后续过程

实际操作：通过生成5000个明文/密文对（对应∆P），模拟得到256个值对应的概率，以下是部分值：

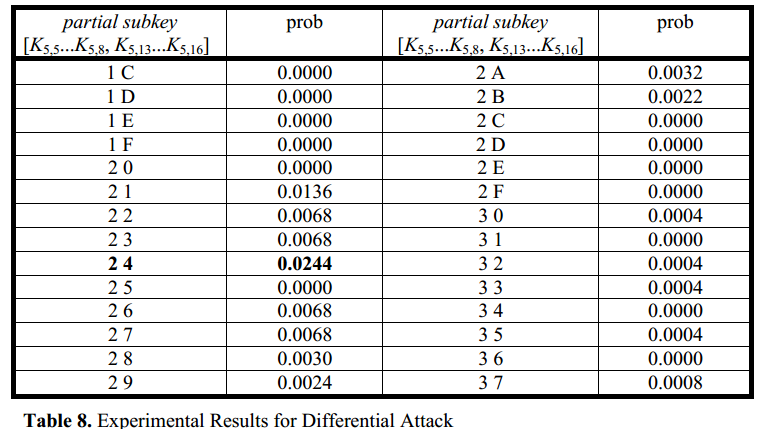
image-20241210194612774

概率最大的是[2 4]，是正确的subkey，但并不等于理想的27/1024

因为有几个因素会影响计数与理论期望不同：

the partial decryption for different partial subkeys 不同部分子密钥的部分解密

the imprecision of the independence assumption required for determination of the characteristic probability 确定特征概率所需的独立性假设的不精确性

the concept that differentials are composed of multiple differential characteristics 微分是由多个微分特征组成的概念

Complexity of the Attack攻击的复杂度

def：对于差分密码分析，我们将具有非零输入差分（因此是非零输出差分）的特征所涉及的S盒称为有源S盒（active S-boxes)

一般来说，active S-boxes的微分概率越大，完整密码的特征概率就越大。同时，active S-boxes越少，特征概率越大。

在考虑密码分析的复杂性时，我们考虑进行攻击所需的数据。也就是说，假设能够获取ND个明文，我们就能够处理它们（攻击者能够获得足够的明文对，并使用这些数据进行分析和攻击）

确定攻击所需的明文对数量的经验法则：

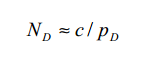
image-20241210200033293

公式正确性的理解：正确配对出现几次就足以使正确的目标部分子密钥的计数显著大于错误目标部分子密钥的计数。由于正确配对大约每 1/pD 个明文对就会出现一次，因此在实际应用中，通常可以使用 1/pD 的小倍数的选定明文对来成功地进行攻击。

c是一个小常数，pD 是 R 轮密码的 R−1 轮的差分特征概率（假设每个活动 S-box 中的差分对是独立的），则：

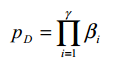
image-20241210200145460

抗差分密码分析的策略主要集中在 S-box 的性质上（即最小化 S-box 的差分对概率）以及寻找结构来最大化活动 S-box 的数量。Rijndael（即 AES）就是一个为提高抗差分密码分析能力而设计的良好密码示例。

注意假设的前提条件：差分特征概率的计算通常假设 S-box 是独立的，但实际情况中 S-box 之间可能存在依赖关系。因此，差分特征概率是一个估算值，虽然在实际中，很多密码的差分特征概率计算仍然是相当准确的。

最重要的是，具有相同输入差分和输出差分（即相同的差分）的不同差分特征可以组合起来，表示一个比单个差分特征所隐含的更大的差分概率。

即多个差分特征（尽管它们各自表示相同的输入和输出差分）可以一起作用，从而导致一个比单个差分特征计算得到的差分概率更高。这是因为不同的差分特征可能会相互“增强”彼此的效果，从而使得综合概率更大。这里提到的概念类似于线性密码分析中的“线性包络”（linear hulls）——多条线性关系（或者特征）结合起来，可以形成更强的攻击效果。

所以，为了证明密码对差分密码分析的安全性，必须证明所有可能的差分组合的概率都低于某个可接受的阈值，而不仅仅是单个差分特征的概率低于某个可接受的阈值。

不过，通常可以合理假设，当一个差分特征具有较高的概率时，它会主导差分的发生，而且该特征的概率可以很好地近似差分的实际概率。

参考文献

Heys, Howard M. “A tutorial on linear and differential cryptanalysis.” Cryptologia 26.3 (2002): 189-221.