Hexo
0%

发表于 分类于

容器和类容器

string

1.string不是容器，但是有跟序列容器类似的成员函数

  • begin和end
  • empty
  • size
  • swap（支持交换）
  • 支持==、<等比较运算

2.string的内存布局

h e l l o ! \0
begin end
front back
  • begin和end是迭代器，类似于指针，end指向末尾+1
  • front和back是引用

3.string其他用法

  • size()的复杂度是O(1)，strlen()的复杂度是O(N)
  • 支持字符串的拼接和查找
  • nops是一个string的常数，当查找不存在的字符时会返回 nops
  • 支持到数字的互转： stoi()和 to_string

序列容器

array

array的特点：

  1. 和C数组一样在栈上分配，性能方面没有差异

  2. 需要编译期确定数组大小

  3. 提供了 begin、 end、 size等通用成员函数

  4. 解决了C数组的怪异行为

    • 不能按值拷贝，具体表现：

      a. 直接赋值：在C中，不能直接将一个数组赋值给另一个数组，int a[5] = {1, 2, 3, 4, 5}; int b[5]; b = a;是非法的，array<int, 5> a = {1, 2, 3, 4, 5}; array<int, 5> b; b = a;是合法的

      b. 函数传参：数组作为函数参数，实际上传递的是指向数组的指针，而不是整个数组的拷贝

    • 作为参数有退化行为，被调用函数不能获得C数组的长度

  5. 支持 == <等比较运算（原生数组不能直接使用比较运算符，此时比较的是两个数组的地址，array、vector会自动逐元素比较数组）

vector

  • 最常用的序列容器
  • 大小可变的动态数组
  • 为尾部增删元素而优化

vector的内存布局

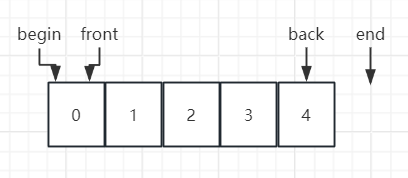
image-20240814142205726

  • begin、end：指针、迭代器
  • front、back：引用

异常安全要求

当 vector 空间不够时，扩容时希望在内存重分配时使用元素的移动构造函数的话，必须声明为 noexcept

否则容器会使用拷贝构造函数

原因：保证强异常安全性，在 vector的 insert、push_back等操作中保证强异常安全性，怎么实现：如果插入的时候空间不够会扩容，在新的内存块中相应的位置构造要求插入的成员，如果失败的话，抛异常并释放内存，如果成功的话，将原先的内存拷贝或者移动过去。如果在移动过程中出现异常，新的内存块没构造完成，旧的内存块被移走，就没办法保证强安全性。 vector保证强异常安全性是指：如果操作失败，能够保证完整的回退到当前插入操作之前的状态。

示例程序：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
class Obj1
{
public:
    Obj1()
    {
        cout << "Obj1()" << endl;
    }
    Obj1(const Obj1 &)
    {
        cout << "Obj1(const Obj1&)" << endl;
    }
    Obj1(Obj1 &&)
    {
        cout << "Obj1(Obj1&&)" << endl;
    }
};
class Obj2
{
public:
    Obj2()
    {
        cout << "Obj2()" << endl;
    }
    Obj2(const Obj2 &)
    {
        cout << "Obj2(const Obj2&)" << endl;
    }
    Obj2(Obj2 &&) noexcept
    {
        cout << "Obj2(Obj2&&)" << endl;
    }
};
// 区别：Obj2的移动构造函数声明为noexcept
int main()
{
    vector<Obj1> v1;
    v1.reserve(2);
    v1.emplace_back();
    v1.emplace_back();
    v1.emplace_back();

    vector<Obj2> v2;
    v2.reserve(2);
    v2.emplace_back();
    v2.emplace_back();
    v2.emplace_back();
};
1
2
3
4
5
6
7
8
9
10
Obj1()
Obj1()
Obj1()
Obj1(const Obj1&)
Obj1(const Obj1&)
Obj2()
Obj2()
Obj2()
Obj2(Obj2&&)
Obj2(Obj2&&)

运行结果：Obj1扩容使用拷贝构造，Obj2扩容使用移动构造

deque

  • 双端队列
  • 为头尾高效增删元素而优化

deque的内存布局

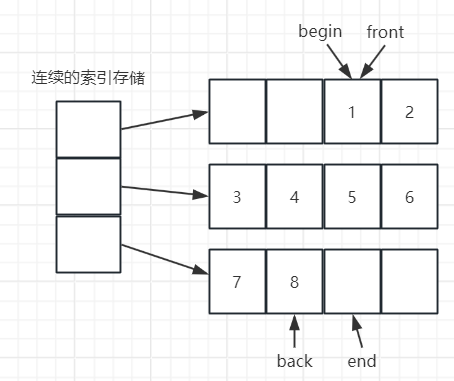
image-20240814144709712

跟 vector 相比的优点：头尾插入的时候不会涉及额外的移动操作，只需要创建一个新的内存块，只有当索引存储不够时才需要移动索引存储，所以当需要在头尾频繁插入数据时，deque是一个性能很高的选择

deque的特点

  1. 只从头尾进行增删时，容器里的对象永远不需要移动
  2. 容器里的元素只是部分连续
  3. 元素的存储大部分仍然连续，遍历性能较高
  4. 支持使用下标访问容器元素，仍能保持O(1)

list

  • 双向链表
  • 为任意位置插入和删除优化

list内存布局：同理，begin和front指向首，back指向尾，end指向尾+1

list的特点

  1. 提供高效的、O(1)复杂度的任意位置的插入和删除操作
  2. 不支持使用下标访问元素
  3. 不支持 sort 算法，但能使用其成员函数 sort，例：sort(list.begin(),list.end())错误，正确：list.sort()

forward_list

  • 单向链表
  • 比 list少了前继结点，比 list 内存占用少

容器适配器

queue

  • 先进先出的容器适配器
  • 底层默认使用 deque，也可以是 list
  • 不能按下标访问，只能从首部弹出，尾部添加

stack

  • 后进先出的容器适配器
  • 底层默认使用 deque，也可以是 list、vector

priority_queue

  • 优先级队列（部分排序的队列），排序的部分在顶部

  • 默认使用 less 排序

  • 排序的末项在顶部，默认是大根堆

  • 模板参数:
_Tp – Type of element.
_Sequence – Type of underlying sequence, defaults to vector<_Tp>.
_Compare – Comparison function object type, defaults to less<_Sequence::value_type>.

priority_queue<int,vector<int>,my_greater> que; // 函数 "my_greater" 不是类型名C/C++(757)
// 所以这里的参数也只能是函数对象

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12

    ------

    **函数对象 `less`**

    ```c++
    template <class T>
    struct less:binary_function<T,T,bool>{
        bool operator()(const T& x,const T& y){
            return x<y;
        }
    }

函数对象：在class或struct中实现 operator() 的对象，生成这样一个对象之后，可以使用 () 来调用函数，行为跟普通函数有点区别

注意：sort可以接受函数指针作为参数，但是 map set只能接受函数对象

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
bool my_greater(int x, int y)
{
    return x > y;
}
vector<int> vec = {4, 5, 2, 3};
sort(vec.begin(), vec.end(), my_greater);
// 5 4 3 2 
sort(vec.begin(), vec.end(), less<int>());
// 2 3 4 5

set<int, less<int>> set{5, 3, 2, 4};
// 2 3 4 5 
set<int, my_greater> set{5, 3, 2, 4};
// 报错：函数 "my_greater" 不是类型名C/C++(757)
模板参数:
_Key – Type of key objects.
_Compare – Comparison function object type, defaults to less<_Key>.
_Alloc – Allocator type, defaults to allocator<_Key>.

关联容器

  • 有序的容器，默认使用 less
  • set、map、multiset、multimap：key是否可重复
  • 查找、插入和删除的时间复杂度都是 O(log N)

无序关联容器

  • 容器元素间没有顺序关系

  • 默认使用 hash，也可以使用自定义的函数对象

    1
    2
    3
    4
    5
    6
    7
    template<typename T>
    struct hash<complex<T>>{
        size_t operator()(const complex<T> &v)const noexcept{
            hash<T> h;
            return h(v.real())+h(v.imag());
        }
    };

  • unordered_set、unordered_map、unordered_multiset、unordered_multimap：key是否可重复

发表于 分类于

图

  • 做题方法：选一个模板，实现所有的算法，遇到具体题目的时候，转化为自己熟悉的结构

拓扑排序

  • 找到入度为0的点进队
  • 每出队一个点，就把该点的影响消除，把nexts的入度减一

最小生成树

无向图，连通且权值和最小

krusal算法

从边来找——>最小的边min

看最小的边加上后是否成环

Q：如何判断是否成环

A：看边连接的两个点是否属于两个集合 哈希map（点，点所在的集合）

prim算法
  • 最小生成堆
  • 每次从解锁的边里选最短的，并且点to未访问
  • 将边cur加入结果，点to加入visited，将点to相邻的边加入小顶堆

最小路径—Dijkstra算法

  • 初始化
    • distanceMap <node* ,int>：指定点到每一个点的距离
      • 先加入<head,0>
    • selectedNodes <node*>：已经访问过的点，即距离已确定，无需再修改
  • 从distanceMap里选择距离最小且未访问的——>minnode
    • 遍历Minnie的边集（从minnode出来的边）
      • 如果distanceMap里没有点to的记录，就加入（点to，distance+weight）
      • 如果有的话，就加入（点to，min{distance+weight，点to的距离}）
    • 把minnode加入selected
    • 找minnode，循环

发表于 更新于 分类于

树

基础遍历

递归遍历

例： 1

​ 2 3

​ 4 5 6 7 

1
2
3
4
5
6
7
8
void Order(node *head){
    if(head==null) return;
    //(1)
    Order(head->left);
    //(2)
    Order(head->right);
    //(3)
}

递归序(访问结点的顺序)：1 2 4 4 4 2 5 5 5 2 1 3 6 6 6 3 7 7 7 1

1
cout<<head->data<<" ";//打印语句位置

先序遍历：第一次访问打印 (1)

中序遍历：第二次访问打印(2)

后序遍历：第三次访问打印(3)

迭代遍历

三种遍历都是用的栈

先序遍历

144. 二叉树的前序遍历

  1. 头先进栈
  2. 当栈不为空，弹出cur
    1. 打印cur
    2. cur右进栈，左进栈
后序遍历

145. 二叉树的后序遍历

  1. 头先进栈
  2. 当栈不为空，弹出cur
    1. 打印cur
    2. cur左进栈，右进栈
  3. 翻转数组
中序遍历

94. 二叉树的中序遍历

  1. 整棵树左边界进栈
  2. 弹出，打印cur
  3. cur右子树的左边界进栈

宽度优先遍历/层次遍历

宽度优先遍历用队列

  1. 头结点先进队
  2. 循环
    1. 弹出就打印cur
    2. 先放左再放右

求二叉树最大宽度

  • 法1：哈希表：（head，1）//第一层

    curlevel,curlevelnode,max

    弹出结点=当前层，node++

    else 说明进入下一层了

    ——>需要一个哈希表，进队列的时候(left，level+1);

  • 法2：队列

常见概念

搜索二叉树

每一个节点大于左子树，小于右子树

判断：中序遍历，输出一定是升序

98. 验证二叉搜索树

完全二叉树

958. 二叉树的完全性检验

满二叉树

平衡二叉树

任何节点左树和右树的高度差都不超过1

二叉树的递归套路

  1. 列出所有的可能性
  2. 整理需要左树、右树提供的信息，封装为结构体，作为返回值（左右子树返回值得是一样的）
  3. 函数结构
    1. 空树情况（如果情况比较奇怪，返回NULL，调用的时候再讨论）
    2. 处理左树，处理右树
    3. 根据左右子树信息，处理本树
    4. 返回

递归套路可以解决一切树型dp问题：问题可以通过向左子树和右子树要信息解决

但要具体问题具体分析，也不是所有问题都能用套路

发表于 分类于

链表

哈希表

unordered_map的使用

既有key又有value就是map结构

  1. 头文件：

    #include< unordered_map>

  2. 定义一个哈希表(我们以Key和Value都是int变量为例)

    unordered_map<int,int> Hash;

  3. 哈希表的建立有下面几种方法

    1
    2
    3
    Hash[1]=3;
    Hash.insert<make_pair(1,3)>;
    Hash.insert({ {1,3},{2,4} });

  4. 迭代器

    unordered_map<int,int>::iterator it;

  5. 利用迭代器访问变量

    it->first; it->second;

  6. 哈希表的查找

    it=Hash.find(1);

  7. 修改哈希表

    Hash[1] = 4;

  8. 清除哈希表

    Hash.erase(1); Hash.clear();

  • 放入哈希表的东西：

    如果是基础类型，内部按值传递，内存占用就是这个东西的大小，如int，string

    Eg：unordered_map<int,int> Hash;unordered_map<string,string> Hash;Hash.insert<make_pair("ssdefefrf",3)>

    ​ string多大则哈希表多大，是把值直接拷贝到哈希表

    如果不是基础类型，内部按引用传递，内存大小就是这个东西内存地址大小，即8字节，如自定义的node

    ​ 不管node多大，哈希表里存放的就是node的地址

  • 哈希表的增删查改操作都是常数级

有序表

哈希表能实现的功能，有序表都能实现

并且有序表的key按某种规则有序组织

有序表的增删查改操作都是O(logN)

放入有序表的东西：

如果是基础类型，内部按值传递，内存占用就是这个东西的大小

如果不是基础类型，内部按引用传递，内存大小就是这个东西内存地址大小，即8字节，并且必须提供比较器

单链表

链表由一系列结点组成

结点=数据+下一个结点的指针

链表的特点：

  1. 存储空间可连续也可不连续
  2. 链表的存取通过头节点开始
  3. 是非随机存取的存储结构

链表的插入方式

image-20240321161019496

插在头节点前还是头节点后

  1. 头插法

    new->next=head;head=new;

  2. 尾插法

    new->next=head->next;head->next=new;

单链表的结构

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
//单链表类的定义
template<class elemType>
class sLinkList{
private:
	struct node{//单链表中的结点类
		elemType data;
		node *next;
		node(const elemType &x,node *n=NULL){//结点构造函数
			data=x;
			next=n;
		}
		node():next(NULL){}//*
		~node(){};//注意要写实现
	};
	node *head;
	int currentLength;
	node *move(int i) const;//返回第i个结点的位置
public:
	sLinkList();
	~sLinkList(){
		clear();
		delete head;
	};
	void clear();
	int length(){
		return currentLength;
	}
	void insert(int i,const elemType &x);
	void remove(int i);
	int search(const elemType &x)const;
	elemType visit(int i) const;
	void traverse() const;
};


//链表构造函数
template<class elemType>
sLinkList<elemType>::sLinkList(){
	head=new node;
	currentLength=0;
}

//清除线性表
template<class elemType>
void sLinkList<elemType>::clear(){
	node *p=head->next,*q;
	head->next=NULL;

	while(p->next!=NULL){
		q=p->next;//先记录p下一个结点
		delete p;//再删除p
		p=q;
	}
	currentLength=0;
}

//返回第i个元素的指针
template<class elemType>
typename sLinkList<elemType>::node *sLinkList<elemType>::move(int i) const{
	node *p=head;
	for(int j=0;j<=i;j++){
		p=p->next;
	}
	return p;
}

//在i处插入x
template<class elemType>
void sLinkList<elemType>::insert(int i,const elemType &x){
	//i-1处的下一个结点是x
	node *pos=move(i-1);
	pos->next=new node(x,pos->next);
	currentLength++;
}

//删除第i个元素
template<class elemType>
void sLinkList<elemType>::remove(int i){
	//i-1处的下一个结点是i+1处
	node *pos=move(i-1);
	node *del=pos->next;
	pos->next=del->next;
	delete del;
	currentLength--;
}

//搜索线性表中是否出现x，找不到返回-1，找到返回x的下标
template<class elemType>
int sLinkList<elemType>::search(const elemType &x)const{
	node *p=head->next;
	for(int i=0;i<currentLength;i++,p=p->next){
		if(p->data==x) return i;
	}
	return -1;
}

//访问线性表的第i个元素
template<class elemType>
elemType sLinkList<elemType>::visit(int i)const{
	return move(i)->data;
}

//遍历运算
template<class elemType>
void sLinkList<elemType>::traverse()const{
	node *p=head->next;
	for(int i=0;i<currentLength;i++,p=p->next){
		cout<<p->data<<" ";
	}
}

//使用
sLinkList<int> list;

双链表

每个结点附加了两个指针字段，previous：前驱节点的地址，next：后继节点的地址

头节点：previous=NULL，next=a[0]

尾结点：previous=a[末]，next=NULL

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
template<class elemType>
class dLinkList{
private:
	struct node{//双链表的结点类
		node *prev,*next;
		elemType data;
		node(const elemType &x,node *p=NULL,node *n=NULL){
			data=x;prev=p;next=n;
		}
		node():prev(NULL),next(NULL){}
		~node(){}
	};
	node *head,*tail;
	int currentLength;
	node *move(int i);//返回i位置的结点
public:
	dLinkList();
	~dLinkList(){
		clear();
		delete head;
		delete tail;
	}
	void clear();
	int length(){
		return currentLength;
	}
	void insert(int i,elemType &x);
	void remove(int i);
	int search(const elemType &x);
	elemType visit(int i);
	void traverse();
};

template <class elemType>
dLinkList<elemType>::dLinkList(){
	head=new node;
	tail=new node;
	head->next=tail;
	tail->prev=head;
	currentLength=0;
}

template <class elemType>
typename dLinkList<elemType>::node *dLinkList<elemType>::move(int i){
	node *p=head;
	for(int j=0;j<=i;j++){
		p=p->next;
	}
	return p;
}

template <class elemType>
void dLinkList<elemType>::insert(int i,elemType &x){
	node *pos=move(i-1);//a[i-1]
	node *next=pos->next;//a[i]
	node *tmp=new node(x,pos,next);
	pos->next=tmp;
	next->prev=tmp;
	currentLength++;
}

template <class elemType>
void dLinkList<elemType>::clear(){
	node *p=head->next,*q;
	head->next=NULL;
	while(p!=NULL){
		q=p->next;
		delete p;
		p=q;
	}
	delete p;
	delete q;
	delete head;
	currentLength=0;
}

template <class elemType>
void dLinkList<elemType>::remove(int i){
	node *pos=move(i-1);
	node *del=pos->next;//a[i]
	node *next=del->next;
	pos->next=next;
	next->prev=pos;
	delete del;
	currentLength--;
}

template <class elemType>
int dLinkList<elemType>::search(const elemType &x){
	node *p=head->next;
	for(int i=0;i<currentLength;i++,p=p->next){
		if(p->data==x) return i;
	}
	return -1;
}
	
template <class elemType>
elemType dLinkList<elemType>::visit(int i){
	return move(i)->data;
}

template <class elemType>	
void dLinkList<elemType>::traverse(){
	node *p=head->next;
	for(int i=0;i<currentLength;i++,p=p->next){
		cout<<p->data<<" ";
	}
}

循环链表

一般单循环链表不设头节点，双循环链表不设头尾结点

题目

笔试：只要求时间复杂度

面试：时间复杂度优先，空间复杂度尽可能小

技巧：1、额外数据结构记录；2、快慢指针

反转链表

给你单链表的头节点 head ，请你反转链表，并返回反转后的链表。

回文链表

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

  • 不要求空间

    • 准备一个栈，遍历链表进栈，出栈==原链表——>回文链表

    • 改进：让链表右边一半进栈

      • Q：怎么知道右边一半开始

        A：准备两个指针，慢指针一次走一步，快指针一次走两步，注意边界条件

  • 要求空间复杂度

    • 准备快慢指针，当慢指针走到中间的时候，把后面的链表逆序，然后一块从两头向中间遍历，最后恢复链表

  • 将单向链表按某值划分为左边小、中间相等、右边大的形式

    • 要求低

      • 定义一个node型的数组，进行partition，再串起来

        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        15
        16
        17
        18
        19
        20
        21
        22
        23
        24
        25
        26
        27
        28
        29
        30
        31
        32
        33
        34
        template<class elemType>
        void sLinkList<elemType>::partition(int aim){
        	node *arr[currentLength];
        	node *pos=head->next;
        	for(int i=0;i<currentLength;i++){
        		arr[i]=pos;
        		pos=pos->next;
        	}
        	int i=0,low=-1,high=currentLength;
        	node *temp;
        	while(i!=high){
        		if(arr[i]->data<aim){
        			temp=arr[i];
        			arr[i]=arr[low+1];
        			arr[low+1]=temp;
        			low++;
        			i++;
        		}
        		else if(arr[i]->data==aim){
        			i++;
        		}
        		else if(arr[i]->data>aim){
        			temp=arr[i];
        			arr[i]=arr[high-1];
        			arr[high-1]=temp;
        			high--;
        		}
        	}
        	head->next=arr[0];
        	for(int i=0;i<currentLength-1;i++){
        		arr[i]->next=arr[i+1];
        	}	
        	arr[currentLength-1]->next=NULL;
        }

    • 要求高

      • 定义六个变量，小于等于大于三个区域的头和尾，最后再连起来

        • 此时的partition具有稳定性
        1
        2
        3
        4
        5
        6
        7
        8
        9
        10
        11
        12
        13
        14
        15
        16
        17
        18
        19
        20
        21
        22
        23
        24
        25
        26
        27
        28
        29
        30
        31
        32
        33
        34
        35
        36
        37
        38
        39
        40
        41
        42
        43
        44
        45
        46
        47
        48
        49
        50
        51
        52
        53
        54
        55
        56
        57
        58
        59
        60
        61
        62
        63
        64
        65
        66
        67
        68
        69
        70
        71
        72
        73
        74
        75
        76
        template<class elemType>
        void sLinkList<elemType>::partition(int aim){
        	node *sh=NULL;
        	node *st=NULL;
        	node *mh=NULL;
        	node *mt=NULL;
        	node *bh=NULL;
        	node *bt=NULL;
        	node *pos=head->next;
        	while(pos!=NULL){
        		if(pos->data<aim){
        			if(sh==NULL){
        				sh=pos;
        				st=pos;
        			}
        			else{
        				st->next=pos;
        				st=pos;
        			}
        		}
        		else if(pos->data==aim){
        			if(mh==NULL){
        				mh=pos;
        				mt=pos;
        			}
        			else{
        				mt->next=pos;
        				mt=pos;
        			}
        		}
        		else if(pos->data>aim){
        			if(bh==NULL){
        				bh=pos;
        				bt=pos;
        			}
        			else{
        				bt->next=pos;
        				bt=pos;
        			}
        		}
        		pos=pos->next;
        	}
        	st->next=NULL;
        	mt->next=NULL;
        	bt->next=NULL;
        	//将三个区域连起来，注意讨论区域为空的情况
        	if(sh==NULL){
        		if(mh==NULL) head->next=bh;
        		else{
        			head->next=mh;
        			if(bh==NULL) mt->next=NULL;
        			else{
        				mt->next=bh;
        				bt->next=NULL;
        			}
        		}
        	}
        	else{
        		head->next=sh;
        		if(mh==NULL){
        			if(bh==NULL) st->next=NULL;
        			else{
        				st->next=bh;
        				bt->next=NULL;
        			}
        		}
        		else{
        			st->next=mh;
        			if(bh==NULL) mt->next=NULL;
        			else{
        				mt->next=bh;
        				bt->next=NULL;
        			}
        		}
        	}
        }

    随机链表的复制

    给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

    构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点 。

    例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。

    返回复制链表的头节点。

    用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

    val：一个表示 Node.val 的整数。

    random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

    你的代码 只 接受原链表的头节点 head 作为传入参数。

    • 要求低：可以使用额外空间，哈希表

      • 哈希表的key=node(old),value=node(new)

        （1）的next指向（2），则value(1)的next指向value（2）

    • 要求高：不使用哈希表

      • 克隆新节点挂在旧结点后面，加上rand指针，old->next->rand=old->rand
      • 分离新旧链表

两个单链表相交的一系列问题

题目：给定两个可能有环也可能无环的单链表，头节点head1/2，函数：若相交返回相交的第一个结点，若不相交，返回null

要求：链表长度之和为N，时间复杂度：O(N)，空间复杂度：O(1)

1.判断环
  • 使用哈希
    • 准备一个set，遍历，set中有无，无则放入，有则说明是入环结点
  • 快慢指针，初始都在头节点，慢指针走一步，快指针走两步
    • 快指针=null——>无环
    • 若有环，则快慢指针一定会相遇
      1. 让快指针回到头节点
      2. 快慢指针每次移动一步，则快慢指针相遇的地方就是入环结点
2.判相交结点
  • 两个都无环
    • if end1!=end2 不相交
    • else 从长链表中*位开始往后走，短链表从头往后中，可得相交结点##
  • 一个有环一个无环，一定不相交
  • 两个都有环
    • loop1？=loop2
      • =，复用##
      • ！=，从loop1能不能走到loop2
        • 不能，不相交
        • 能，loop1和loop2都是相交结点

发表于 分类于

O(NlogN)的排序

归并排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void mergeSort(int arr[],int n){
	sort(arr,0,n-1);
}

void sort(int arr[],int l,int r){
	if(l==r) return;
	int mid=l+((r-l)>>1);
	sort(arr,l,mid);
	sort(arr,mid+1,r);
	merge(arr,l,mid,r);
}

void merge(int arr[],int left,int mid,int right){
	int p1=left,p2=mid+1,current=0;
	int result[right-left+1];
	while(p1<=mid&&p2<=right){
		if(arr[p1]<=arr[p2]){
			result[current++]=arr[p1++];
		}
		else{
			result[current++]=arr[p2++];
		}
	}
	while(p1<=mid) result[current++]=arr[p1++];
	while(p2<=right) result[current++]=arr[p2++];
	for(int i=0;i<right-left+1;i++){
		arr[left+i]=result[i];
	}
}

时间复杂度O(NlogN)

时间复杂度比插入选择排序小，因为原来的比较n次只得到一个结果，下一轮重新开始比较，而归并排序把每一次的比较结果都传递给了下一轮；

空间复杂度大，因为多定义了一个数组

扩展

小和问题

在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int merge(int arr[],int left,int mid,int right){
	int p1=left,p2=mid+1,current=0,sum=0;
	int result[right-left+1];
	while(p1<=mid&&p2<=right){
		if(arr[p1]<arr[p2]){
			sum=sum+arr[p1]*(right-p2+1);
			result[current++]=arr[p1++];	
		}
		else if(arr[p1]>arr[p2]){
			result[current++]=arr[p2++];
		}
		else result[current++]=arr[p2++];
	}
	while(p1<=mid) result[current++]=arr[p1++];
	while(p2<=right) result[current++]=arr[p2++];
	for(int i=0;i<right-left+1;i++){
		arr[left+i]=result[i];
	}
	return sum;
}

int SmallSum(int arr[],int l,int r){
	if(l==r) return 0;
	int mid=l+((r-l)>>1);
	return SmallSum(arr,l,mid)+SmallSum(arr,mid+1,r)+merge(arr,l,mid,r);
}

int getSmallSum(int arr[],int n){
	return SmallSum(arr,0,n-1);
}
逆序对问题

在一个数组中，左边的数如果比右边的数大，则折两个数构成一个逆序对，请输出逆序对的个数。

LCR 170. 交易逆序对的总数

在股票交易中，如果前一天的股价高于后一天的股价，则可以认为存在一个「交易逆序对」。请设计一个程序，输入一段时间内的股票交易记录 record，返回其中存在的「交易逆序对」总数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
int mergeReverse(vector<int>& record,int left,int mid,int right){
    int p1=left,p2=mid+1,p=0,result=0;
    int help[right-left+1];
    while(p1<=mid&&p2<=right){
        if(record[p1]>record[p2]){
            result=result+(right-p2+1);
            help[p]=record[p1];
            p++;
            p1++;
        }
        else{
            help[p]=record[p2];
            p++;
            p2++;
        }
    }
    while(p1<=mid){
        help[p]=record[p1];
        p++;
        p1++;
    }
    while(p2<=right){
        help[p]=record[p2];
        p++;
        p2++;
    }
    for(int i=0;i<=right-left;i++){
        record[left+i]=help[i];
    }
    return result;
}

int getReverse(vector<int>& record,int left,int right){
    if(left==right) return 0;
    int mid=left+((right-left)>>1);
    return getReverse(record,left,mid)+getReverse(record,mid+1,right)+mergeReverse(record,left,mid,right);
}

int reversePairs(vector<int>& record) {
    if(record.size()==0) return 0;
    return getReverse(record,0,record.size()-1);
}

快排

快排1.0

小于等于num + 大于num

时间复杂度：O(N^2)，原因：划分值num打的很偏，导致只有一侧

快排2.0

小于num + 等于num + 大于num

时间复杂度：O(N^2)，原因：划分值num打的很偏，导致只有一侧

快排3.0

随机选择一个数与最后一位数做交换，再作为划分值——>好情况和坏情况是概率事件，每种情况只占1/N，求每种情况时间复杂度的数学期望

时间复杂度：O(NlogN)

空间复杂度：O(logN) 最差是O(N) <——递归（记录中点位置）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
//快排，num,等于区域：p[0],p[1]
//[i]<num,与小于边界的右边一位交换，i++，边界++
//[i]=num,i++
//[i]>num,与大于边界的左边一位交换，边界--
vector<int> partition(int arr[],int l,int r){//返回等于区的左右边界
	//以最后一个数作为划分值
	int low=l-1;//小于区左边界
	int high=r;//等于区右边界	
	int i=l;//当前数的位置
	while(i<high){
		if(arr[i]<arr[r]){
			swap(arr,i,low+1);
			low++;
			i++;
		}
		else if(arr[i]==arr[r]){
			i++;
		}
		else{
			swap(arr,i,high-1);
			high--;
		}
	}
	swap(arr,high,r);
	return {low+1,high};
}

void quickSort(int arr[],int l,int r){
	if(l<r){
		//随机选取一个数与最后一个数交换
		srand(time(0));
		int idx=(rand()%(r-l+1))+l;
		swap(arr,idx,r);
		vector<int> p=partition(arr,l,r);
		quickSort(arr,l,p[0]-1);
		quickSort(arr,p[1]+1,r);
	}
}

扩展

荷兰旗问题

75. 颜色分类

给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ，**原地**对它们进行排序，使得相同颜色的元素相邻，并按照红色、白色、蓝色顺序排列。

我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。

必须在不使用库内置的 sort 函数的情况下解决这个问题。

堆排

堆

完全二叉树：从上到下从左到右依次排满的过程

数据结构：从0开始的连续数组

父节点：(i-1)/2

左节点：2i+1，右节点：2i+2

大根堆/小根堆：根节点最大/最小

Q：插入一个数

1
2
3
4
5
6
7
8
//插到数组最后，不断与父节点比较，若大于父节点则交换
//不断向上移动直到来到合适的位置
void heapInsert(int arr[],int idx){//让idx来到正确的位置
	while(arr[idx]>arr[(idx-1)/2]){
		swap(arr,idx,(idx-1)/2);
		idx=(idx-1)/2;
	}
}

Q：去掉最大值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//把最后一个数移到根节点处，然后不断下移直到合适的位置
//下移：不断与左右节点最大的交换，直到没有子节点或者大于子节点
void heapify(int arr[],int idx,int heapsize){//从idx开始下移
	int max;
	while(2*idx+1<heapsize){
		max=2*idx+1;
		if(2*idx+2<heapsize&&arr[max]<arr[2*idx+2]){
			max=2*idx+2;
		}
		if(arr[max]<arr[idx]) break;
		swap(arr,idx,max);
		idx=max;
	}
}

堆排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void heapSort(int arr[],int n){
    //创建大根堆，一个个插入
	for(int i=0;i<n;i++){
		heapInsert(arr,i);
	}
	int heapSize=n;
    //arr[0]跟arr[末]交换=最大值来到了最后
	swap(arr,0,heapSize-1);
	heapSize--;
	while(heapSize>0){
		heapify(arr,0,heapSize);
		swap(arr,0,--heapSize);
	}
}

时间复杂度O(NlogN)

空间复杂度O(1)

1
2
3
4
//创建大根堆的优化：从下往上从右往左不断heapify
for(int i=n-1;i>=0;i--){
    heapify(nums,i,n);
}

桶排序

计数排序

Q：员工年龄排序（0~200）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
//i位置表示i岁的员工个数
void countSort(int arr[],int n){
	int num[200]={0};
	for(int i=0;i<n;i++){
		num[arr[i]]++;
	}
	for(int i=0;i<200;i++){
		while(num[i]>0){
			cout<<i<<" ";
			num[i]--;
		}
	}
}
in

局限性：不基于比较的排序，取决于数据状态，比如说年龄范围0~200，准备num[200]，所以得知道数范围

基数排序/桶排序

Eg：[17,13,25,100,72]

  1. 补全[017,013,025,100,072]

  2. 准备十个桶，几进制就几个桶

  3. 按个位进桶

    0 1 2 3 4 5 6 7 8 9
    100 072 013 025 017

    先进先出，按个位出桶[100,072,013,025,017]

  4. 按十位进桶

    0 1 2 3 4 5 6 7 8 9
    100 013
    017    		 025 072

    先进先出，按十位出桶[100,013,017,025,072]

  5. 按百位进桶

    0 1 2 3 4 5 6 7 8 9
    013
    017
    025
    072    		 100

    先进先出，按百位出桶[013,017,025,072,100]

发表于 分类于

简单排序

选择排序

时间复杂度：O(N^2)

1
2
3
4
5
6
7
8
9
10
int minidx,temp;
for(int i=0;i<n;i++){
    minidx=i;
    for(int j=i;j<n;j++){
        if(arr[minidx]>arr[j]) minidx=j;
    }
    temp=arr[i];
    arr[i]=arr[minidx];
    arr[minidx]=temp;
}

冒泡排序

时间复杂度：O(N^2)

1
2
3
4
5
6
7
8
9
10
11
12
13
bool flag=0;//是否冒泡
for(int i=n-1;i>=0;i--){
    flag=0;
    for(int j=0;j<i;j++){
        if(arr[j]>arr[j+1]){
            temp=arr[j];
            arr[j]=arr[j+1];
            arr[j+1]=temp;
            flag=1;
        }
    }
    if(!flag) break;
}

  • 异或：相同为0，不同为1 = 不进位相加

  • 性质：

    1. 0^N = N ;N^N = 0

    2. 满足交换律和结合律 a^b=b^a;a^b^c=a^(b^c)

      a=a^b;b=a^b;a=a^b;

      跑完的结果：a、b交换；前提：a和b在内存中是两块独立的空间，即a指向的内存 != b指向的内存

      eg:a[0]=a[0]^a[0];a[0]=a[0]^a[0];a[0]=a[0]^a[0];

      结果：a[0]变成0

  • 异或相关题目

    Q：在一个整型数组中，只有一个数出现了奇数次，其他数都出现了偶数次

    要求：时间复杂度O（N），空间复杂度O（1）：即使用有限几个变量

    1. 怎么找到这个这个出现了奇数次的数

      1
      2
      3
      4
      5
      //全部异或
      int answer=arr[0];
      for(int i=1;i<n;i++){
          answer=answer^arr[i];
      }

    2. 若只有两个数出现了奇数次呢

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      int temp=0;
      for(int i=0;i<n;i++){
          temp=temp^arr[i];
      }//temp=a^b!=0——>temp至少有一位是1
      int rightOne=temp&(~temp+1);//原码&补码得到最右侧的1

      int temp1=0;
      for(int i=0;i<n;i++){
          if((arr[i]&rightOne)==rightOne){//在某位上为1的才参加异或
              temp1=temp1^arr[i];
          }
      }
      int answer1=temp1;
      int answer2=temp^temp1;

      ps：int rightOne=temp&(~temp+1);//原码&补码得到最右侧的1

插入排序

思想：将新的数插到原来有序数组中合适的位置

1
2
3
4
5
6
7
8
9
int tmp;
for(int i=1;i<n;i++){
    //0~i-1为有序，0~i为想有序
    for(int j=i-1;j>=0&&arr[j]>arr[j+1];j--){
        tmp=arr[j];
        arr[j]=arr[j+1];
        arr[j+1]=tmp;
    }
}

二分法

有序数组中找某个数是否存在

二分查找，时间复杂度 O（log N）

有序数组中找>=某个数最左侧的位置

1
2
3
4
5
6
7
8
9
10
11
12
13
int aim=4;//找到大于等于3最左侧的索引
int low,mid,high,idx=n;//idx记录答案索引
low=0;high=n;
while(low<=high){
    mid=(low+high)/2;
    if(a[mid]<aim){
        low=mid+1;
    }
    else{
        if(mid<idx) idx=mid;
        high=mid-1;
    }
}

局部最小值问题

arr中，无序但任意相邻数不相等，求一个局部最小的位置，要求时间复杂度好于O（N）

局部最小def：0位置比1位置小 / n-1位置比n-2位置小 / i位置比i-1和i+1位置小

1
2
3
4
5
6
7
8
判断0位置和n-1位置是否为局部最小
若不存在，则0↘↙n-1，则0~n-1之间必存在局部最小 
判断中间位置是否为局部最小，
    若是则直接返回
    若不是，
    	if(m-1↗m↖m+1) 则左右侧都存在局部最小
        if(m-1↗m↗m+1) 则左侧一定存在局部最小
        if(m-1↘m↘m+1) 则右侧一定存在局部最小

所以，二分法不一定只能用于有序数组，取决于研究的问题

发表于 分类于

有序表 并查集

问题引入

题目：一个矩阵中只有0和1两种值，每个位置都可以和自己的上、下、左、右四个位置相连，如果有一片1连在一起则成为一个岛，求一个矩阵中有几个岛

1
2
3
4
5
{0,0,1,0,1,0
1,1,1,0,1,0
1,0,0,1,0,0
0,0,0,0,0,0}
这个矩阵有3个岛

【进阶】如何设计一个并行算法解决

200. 岛屿数量 - 力扣（LeetCode）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int numIslands(vector<vector<char>>& grid) {
    int m=grid.size();
    int n=grid[0].size();
    int result=0;
    for(int i=0;i<m;i++){
        for(int j=0;j<n;j++){
            if(grid[i][j]=='1'){
                result++;
                inflect(grid,m,n,i,j);
            }
        }
    }
    return result;
}

void inflect(vector<vector<char>>& grid,int m,int n,int i, int j){
    if(i>=m||i<0||j>=n||j<0||grid[i][j]!='1') return;
    grid[i][j]='2';
    inflect(grid,m,n,i-1,j);
    inflect(grid,m,n,i+1,j);
    inflect(grid,m,n,i,j-1);
    inflect(grid,m,n,i,j+1);
}

【进阶】===》并查集

并查集

操作 ：

  1. bool isSameSet(a,b)
  2. void union(a,b)

很多结构都可以，但只有并查集两种操作的时间复杂度都是O(1)

  1. bool isSameSet(a,b)

    判断a和b的父节点是否相同

  2. void union(a,b)

    判断a和b的父节点是否相同，若不同，个数少的集合的顶端挂在个数多的集合顶端之下

findHead(Element a)：往上走找代表结点

改进：往上走的路径记录下来，路径上的结点直接指向父节点

结论：当findHead调用次数逼近或者大于O(N)，时间复杂度趋近于O(1)——越用越快

C++11的for循环有了一种新的用法：

1
2
3
for (auto n : arr){
	std::cout << n << std::endl;
}

上述方式是只读，如果需要修改arr里边的值，可以使用for(auto& n:arr)，for循环的这种使用方式的内在实现实际上还是借助迭代器的，所以如果在循环的过程中对arr进行了增加和删除操作，那么程序将对出现意想不到的错误。

实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <iostream>
#include <list>
#include <unordered_map>
#include <unordered_set>
#include <stack>
using namespace std;

class UnionFindSet {
private:
	int findHead(int element) {
		stack<int> path;
		while (element != fatherMap.at(element)) {
			path.push(element);
			element = fatherMap[element];
		}
		while (!path.empty()) {
			fatherMap[path.top()] = element;
			path.pop();
		}
		return element;
	}
public:
	unordered_set<int> set;
	unordered_map<int, int> fatherMap;
	unordered_map<int, int> sizeMap;
	UnionFindSet(list<int> dataList) {
		for (int value : dataList) {
			set.emplace(value);
			fatherMap.emplace(make_pair(value, value));
			sizeMap.emplace(make_pair(value, 1));
		}
	}

	bool isSameSet(int a, int b) {
		if (set.count(a) && set.count(b)) {
			return findHead(a) == findHead(b);
		}
		return false;
	}
	void Union(int a, int b) {
		if (set.count(a) && set.count(b)) {
			int afather = findHead(a);
			int bfather = findHead(b);
			if (afather != bfather) {
				int big = sizeMap[afather] >= sizeMap[bfather] ? afather : bfather;
				int small = big == afather ? bfather : afather;
				fatherMap[small] = big;
				sizeMap[big] = sizeMap[afather] + sizeMap[bfather];
				sizeMap.erase(small);
			}
		}
	}
};

进阶解法：设计一个并行算法解决

image-20240624211209801

问题：左右两个cpu分别感染，左侧cpu会识别两个岛，右侧cpu会识别两个岛，原因：破坏了岛的连通性

左右cpu分别计算的结果：4个岛，接下来进行合并

image-20240624211209801

合并方法：

  1. 记录初始感染点（图中绿色），记录边界上被感染点的初始感染点是谁（红色）
  2. 四个初始感染点，记为4个集合{A}{B}{C}{D}
  3. 比较在边界上相连的感染点
    1. 感染点分别为A和C，不在一个集合，进行合并：{AC}{B}{D}，岛数=4-1=3
    2. 感染点为B和C，不在一个集合，进行合并：{ABC}{D}，岛数=3-1=2
    3. 感染点为B和D，不在一个集合，进行合并：{ABCD}，岛数=2-1=1
    4. 感染点为A和D，在一个集合，无需操作
  4. 最后，总岛数=1

如果使用很多个CPU，同样的做法：每个CPU分别感染+记录边界上的感染点

发表于 更新于 分类于

智能指针

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
template <typename T>
class smart_ptr
{
public:
    explicit smart_ptr(T *ptr = nullptr) : ptr_(ptr) {}
    ~smart_ptr() { delete ptr_; }
    T *get() const { return ptr_; }

    // 重载运算符，让行为更像指针
    T &operator*() const { return *ptr_; }
    T *operator&() const { return ptr_; }
    operator bool() const { return ptr_; }

    // // 禁止拷贝，至少可以防止double delete的行为
    // smart_ptr(const smart_ptr &) = delete;
    // smart_ptr &operator=(const smart_ptr &) = delete;
    // // 但禁止拷贝不太方便

    // 希望在拷贝时自动移动资源
    smart_ptr(smart_ptr &other)
    {
        ptr_ = other.release();
    }
    smart_ptr &operator=(smart_ptr &rhs)
    {
        // 拷贝+交换的惯用法，实际上是移动+交换
        // 相当于先将rhs的资源转移给这个临时对象，再把这个临时对象的资源给this
        smart_ptr(rhs).swap(*this);
        return *this;
    }
    T *release()
    {
        T *ptr = ptr_;
        ptr_ = nullptr;
        return ptr;
    }
    void swap(smart_ptr &rhs)
    {
        swap(ptr_, rhs.ptr_);
    }

private:
    T *ptr_;
};

存在危险行为

1
2
3
4
5
6
7
8
9
template <typename T>
void print_addr(smart_ptr<T> ptr)
{
    cout << "Real address of shape is " << static_cast<void *>(&*ptr) << endl;
}
...
smart_ptr<int> ptr(new int(3));
print_addr(ptr);
cout << "Now address of shape is "<< static_cast<void *>(&*ptr) << endl;
1
2
Real address of shape is 0xe22130
Now address of shape is 0

问题： ptr 变成了空指针，原因： print_addr 为值传递，调用函数 smart_ptr(smart_ptr &other) ，将 ptr 传进函数内部对象并置空，离开作用域内部对象被销毁。

危险行为： auto_ptr

右值引用改进——> unique_ptr

1
2
3
4
5
6
7
8
9
10
11
 // 移动构造函数
smart_ptr(smart_ptr &&other)
{
    ptr_ = other.release();
}
// 在进入赋值函数时，先构造一个新的rhs(根据构造函数功能进行构造，拷贝/移动)
smart_ptr &operator=(smart_ptr rhs)
{
    rhs.swap(*this);
    return *this;
}
1
2
3
4
5
6
7
smart_ptr<int> ptr1{new int(2)};
smart_ptr<int> ptr2{ptr1};  // 编译错误
smart_ptr<int> ptr3;
ptr3=ptr1;					//编译错误
ptr3=move(ptr1);
smart_ptr<int> ptr4{move(ptr3)};
// 无法引用 函数 "smart_ptr<T>::smart_ptr(const smart_ptr<int> &) [其中 T=int]" (已隐式声明) -- 它是已删除的函数

完善行为：子类指针向基类转换

1
2
3
4
5
6
7
8
9
10
11
12
// 子类指针向基类转换
template <typename U>
smart_ptr(smart_ptr<U> &&other)
{
    ptr_ = other.release();
}
......// 编译错误：invalid conversion from 'A*' to 'B*'
smart_ptr<A> ptr1(new A());
smart_ptr<B> ptr2=move(ptr1);
......// 编译成功：子类指针可以转换为基类指针
smart_ptr<B> ptr1(new B());
smart_ptr<A> ptr2=move(ptr1);

unique_ptr实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
#include <iostream>
using namespace std;

template <typename T>
class smart_ptr
{
public:
    explicit smart_ptr(T *ptr = nullptr) : ptr_(ptr) {}
    ~smart_ptr()
    {
        delete ptr_;
        // cout << "析构函数" << endl;
    }
    T *get() const { return ptr_; }

    // 重载运算符，让行为更像指针
    T &operator*() const { return *ptr_; }
    T *operator&() const { return ptr_; }
    operator bool() const { return ptr_; }

    // 禁止拷贝，至少可以防止double delete的行为
    smart_ptr(const smart_ptr &) = delete;
    smart_ptr &operator=(const smart_ptr &) = delete;

    // 移动构造函数
    smart_ptr(smart_ptr &&other)
    {
        ptr_ = other.release();
    }
    // 在进入赋值函数时，先构造一个新的rhs(根据构造函数功能进行构造，拷贝/移动)
    smart_ptr &operator=(smart_ptr rhs)
    {
        rhs.swap(*this);
        return *this;
    }
    // 子类指针向基类转换
    template <typename U>
    smart_ptr(smart_ptr<U> &&other)
    {
        ptr_ = other.release();
    }

    T *release()
    {
        T *ptr = ptr_;
        ptr_ = nullptr;
        return ptr;
    }
    void swap(smart_ptr &rhs)
    {
        swap(ptr_, rhs.ptr_);
    }

private:
    T *ptr_;
};

shared_ptr实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
template <typename T>
class smart_ptr
{
public:
    // 构造函数
    explicit smart_ptr(T *ptr = nullptr) : ptr_(ptr)
    {
        if (ptr)
            shared_count_ = new shared_count();
    }
    // 析构函数
    ~smart_ptr()
    {
        // 如果ptr不为空并且引用计数减1之后为空释放资源
        if (ptr_ && !shared_count_->reduce_count())
        {
            delete ptr_;
            delete shared_count_;
        }
    }
    // 特别：除了提供模板化的拷贝构造以外还要提供非模板的拷贝构造
    // 原因：C++不认为下面这种形式的拷贝构造为拷贝构造，所以会生成默认的拷贝构造函数（这种实现实际是错误的）
    // 所以：需要实现非模板的拷贝构造
    smart_ptr(const smart_ptr &other)
    {
        ptr_ = other.ptr_;
        if (ptr_)
        {
            other.shared_count_->add_count();
            shared_count_ = other.shared_count_;
        }
    }
    // 但不需要提供移动构造函数，因为C++发现提供了拷贝构造函数，也不会默认生成移动构造函数

    // 带模板的拷贝构造：实现子类向基类的转换
    template <typename U>
    smart_ptr(const smart_ptr<U> &other)
    {
        ptr_ = other.ptr_;
        if (ptr_)
        {
            other.shared_count_->add_count();
            shared_count_ = other.shared_count_;
        }
    }
    // 带模板的移动构造
    template <typename U>
    smart_ptr(smart_ptr<U> &&other)
    {
        ptr_ = other.ptr_;
        if (ptr_)
        {
            shared_count_ = other.shared_count_;
            other.ptr_ = nullptr;
        }
    }

private:
    T *ptr_;
    shared_count *shared_count_;
};

方便创建智能指针的工具函数

  • make_unique

    • 语义明确，减少重复
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    auto ptr_int = make_unique<int>(42);

    // 如果对象是结构体
    struct Point{
        int x;
        int y;
    };
    auto ptr_point = make_unique<Point>(new Point{1,2}); // 有重复
    // C++20
    auto ptr_point = make_unique<Point>(1,2);

  • make_shared

    • 对象和引用计数一起只进行一次内存分配，提高性能

其他智能指针特性

  • 数组支持
    • unique_ptr<T[]>(C++11)
    • shared_ptr<T[]>(C++17) // C++17之前管理数组需要自定义删除器来释放内存，因为默认使用 delete 不能正确释放分配的数组，需要在自定义删除器中使用 delete[] 释放数组，C++17以后 shared_ptr<T[]> 默认使用 delete[] 来释放管理的对象
  • 自定义删除器
    • 定制智能指针离开作用域之后如何删除管理的对象
    • 作用：在智能指针释放对象时进行一些特殊操作，比如打印日志、管理内存以外的其他资源比如说：文件句柄、数据库连接
    • 使用：可以是函数/类的对象/ lambda表达式
  • weak_ptr
    • 循环引用问题：如果父节点管理子节点，使用 shared_ptr 指向子节点，此时子节点不可以用 shared_ptr 指向父节点，会形成环状依赖，引用计数不会降到0 。此时子节点可以使用 weak_ptr 指向父节点，这样可以保证引用计数最后会降为0，正常析构。
    • 如果可以确定，子节点存在，父节点一定存在的话（不会出现指针悬空），可以考虑使用裸指针，性能更高，使用 weak_ptr 还是有引用计数增减的问题，性能还是有一点影响

智能指针的使用建议

  1. 在指针具有拥有权的时候应当使用 unique_ptr 和 share_ptr
  2. 尽量使用 unique_ptr，一定需要引用计数才用 share_ptr
  3. 注意对智能指针进行拷贝构造或者赋值会影响对象的生命周期（因为这些操作会改变与智能指针相关的引用计数），进而影响所管理对象的生命周期
  4. 传参一般仍使用普通指针或引用，除非要传递所有权

发表于 更新于 分类于

移动语义与右值引用

1.值类别

1）左值

  • 具名，可取地址
  • 非常 non-const左值可以放在赋值运算符的左侧
  • 常见情况
    • 变量
    • 左值对象的成员
    • 返回左值引用的表达式，如 ++x、x = 1
    • 字符串字面量，如 "abc"
      • 字符串字面值为左值一个最重要的原因是可以获取其地址，cout << &"abc" <<endl; 可以正常编译并运行。这是因为C++将字符串左值实现为 char型数组，为其分配了空间并且允许程序员对其进行操作

2）纯右值

  • 不具名、不能取地址的“临时对象”
  • 不可以放在赋值运算符的左侧
  • 常见情况
    • 返回类型非引用的函数调用或运算符表达式，如 x++、 1 + 2
    • 除字符串字面量外的字面量，如 true、 42
    • lambda表达式

3）将亡值

  • C++11引入，和纯右值合称为“右值”
  • 不可以放在赋值运算符的左侧
  • 常见情况
    • 右值对象或者数组的成员
    • 返回右值引用的表达式，如 move(x)——转换为右值引用 若x是int，则move(x)是int &&

2.重要的成员函数重载

1
2
3
4
5
6
7
// 拷贝，当传入参数为左值时调用拷贝构造
T::T(const T& rhs);
T& T::operator=(const T& rhs);

// 移动，当传入参数为右值时调用移动构造
T::T(T&& rhs);
T& T::operator=(T&& rhs);

3.移动的意义

  • 允许资源的传递
  • 允许返回大对象和容器
    • 一般同时使用异常来表示错误

4.移动和 noexcept

noexcept表示函数不会抛出异常

下列成员函数一般不允许抛出异常

  • 析构函数
  • 移动构造函数，如果移动构造没有标成 noexcept，比如说 vector在动态调整大小的时候都不会调用移动构造在移动元素
  • 移动赋值运算符
  • 交换函数（swap）

5.五法则

因为用户定义析构函数、拷贝构造函数、拷贝赋值运算符的存在阻止移动构造函数和移动赋值运算符的隐式定义，所以任何想要移动语义的类应当声明全部五个特殊成员函数。

6.右值引用的误用

1
2
3
4
5
6
7
8
9
10
Obj&& wrong_move(){
    Obj obj;
    return move(obj);// 未定义的行为
}// 返回栈上对象的指针或者引用永远都是错的，不管是左值还是右值

Obj bad_move(){
    Obj obj;
    return move(obj);
}
// 如果要返回函数内部即栈上的对象，直接return obj就行

7.坍缩规则和转发引用

Q：Vector(Vector&& rhs)这里的 rhs是左值还是右值？

A：右值引用变量有标识符，所以是左值

——所以使用右值引用调用其他函数需要加上 move()保持右值属性

Q：在通用的函数模板里怎么办？

A：分别写两个不同的重载

1
2
3
4
5
6
7
8
9
template<typename T>
void bar(T &s){
    foo(s);
}

template<typename T>
void bar(T &&s){
    foo(move(s));
}

问题：重复、啰嗦

引入转发引用

  1. 坍缩规则

    T& & → T&、T& && → T&、T&& & → T&、T&& && → T&&

    所以只有 T&& &&会转化为右值引用

  2. 所以 T&&不是右值引用，当其出现在函数模板的参数或者变量声明中时 T&&是转发引用

  3. std::move(x)：把x转换成右值引用

  4. std::forward<T>(x)：保持x的引用类型——传进来的T是左值，进函数的也是左值，右值也一样

1
2
3
4
5
6
7
8
9
10
11
// forward使用示例
template<typename T>
void bar(T&& s){
    foo(std:forward<T>(s));
}// 不用写两个重载

int main(){
    circle temp;
    bar(temp);
    bar(circle());
}

8.临时对象的生命周期

1
2
3
4
5
class result;
result process_shape(const shape&,const shape&);

process_shape(circle(),triangle());
// circle triangle result 对象在这条语句执行完成后销毁

**生命期延长规则 **

  • 如果一个 prvalue(纯右值) 被绑定到一个引用上，它的生命周期会延长到跟这个引用变量一样长

    result&& r=process_shape(circle(),triangle());

    则右边这个临时对象的生命周期会延长到 r 离开作用域

  • 如果是 xvalue(将亡值) ，则不能延长

    result&& r=move(process_shape(circle(),triangle())); 这种写法是错误的

C++对象的自动生命周期

  1. 后创建的先析构
  2. 全局对象和静态对象在进入 main 之前创建
  3. 函数静态对象在第一次执行到声明语句时创建
  4. 函数自动对象在定义时创建，到定义的所在的 } 即析构
  5. 临时对象在当前语句执行完成后即析构（除非赋值给引用变量而延长生命期）

经典习题：析构顺序

1
2
3
4
5
6
7
8
9
C c;
int main(){
    A *pa=new A();
    B b;
    static D d;
    delete pa;
}
c pa b d 
~pa ~b ~d ~c

发表于 更新于 分类于

资源管理和对象的基本原则

C++的特点与演化

  1. 为什么要使用C++？
    1. 贴近硬件：
      • 使用原生的指令和类型，高性能
      • 方便使用硬件（GPU、FPGA等）
    2. 零开销抽象
      • 类、继承、模板
      • 零开销！=无开销， 零开销=无额外开销
  2. C和C++
    1. 功能上，C++是C的超集
    2. C++更加严格和安全，比如说const的正确性、指针的自动转换
    3. 现代C++的惯用法和C大相径庭
      • C和机器码有更简单的映射关系，从C源码可以大致知道机器码是什么样
      • C++里有更多的抽象机制，源代码和机器码映射复杂得多

资源管理和对象的基本原则

1. 堆与栈

栈的示例

main对应的x86汇编代码（msvc）

  1. 设置栈框架：保存原有的ebp的值，设置新的ebp的值，ebp的作用：索引这个函数所用到的参数和本地变量
  2. 参数压栈
  3. call：调用bar函数，名字奇怪的原因：编译器会起名
  4. 退栈：esp的指针+4——pop eax：取出数据，ESP指向栈中下一个元素
  5. 异或操作对eax寄存器清零，函数返回值存储在eax寄存器

bar对应的x86汇编代码（msvc）

调用过程中的栈变化

“返回main的地址”：main下一句指令的地址

栈内存的特性：

  1. 分配简单，只是移动栈指针
  2. 当前函数执行完即自动释放
  3. 后进先出，不可能出现内存碎片
  4. 函数返回后，栈上对象即被销毁
  5. 栈内存不分享，栈上对象通常没有多线程竞争问题（除非把指向栈内存的指针传递给另一个线程）

堆内存的特性：

  1. 分配和释放算法较为复杂
  2. 可能出现内存碎片
  3. 内存的分配和释放通常需要加锁
  4. 堆上的对象在被释放之前一直可以使用
  5. 堆上对象可能被多个线程访问，潜在有线程竞争问题

2. RAII

——析构函数和RAII是C++最基本的惯用法

  • RAII：Resource Acquisition Is Initialization

  • 帮助管理堆上的对象：对象很大、对象的大小在编译时不能确定、对象是函数的返回值但由于特殊的原因不应使用对象的值返回

  • new和delete的原理

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    // new circle(...)
    {
        void *temp=operator new(sizeof(circle));	//分配内存
        try{
            circle *ptr=static_cast<circle*>(temp);	//类型转换
            ptr->circle(...);						//通过指针调用构造函数
            return ptr;
        }
        catch(...){
            operator delete(ptr);
            throw;
        }
    }
    // delete ptr
    if(ptr!=nullptr){
        ptr->~shape();
        operator delete(ptr);
    }